طیف‌ سنجی مشتق

طیف سنجی مشتق

در طیف‌سنجی مشتق از مشتق اول و یا مشتق‌های مراتب بالاترِ طیف جذب برای تجزیه و تحلیل کمی و کیفی طیف UV-Vis استفاده می‌شود. مفهوم اطلاعات طیف مشتق و مزایای استفاده از آن برای اولین بار در دهه ۱۹۵۰ مطرح شد. اما در ابتدا به دلیل پیچیدگی مشتق‌گیری از طیف و با توجه به اسپکتروفتومترهای آن زمان، توجه زیادی به این روش نشد. سرانجام در اواخر دهه ۱۹۷۰ با ورود ریزرایانه‌ها استفاده از روش‌های ریاضی برای به دست آوردن طیف مشتق با سرعت زیاد، به راحتی و با قابلیت تکرار گسترش یافت.
طیف‌سنجی مشتق یکی از تکنیک‌های طیف‌سنجی است. این تکنیک عمدتا برای تفکیک طیف‌های IR، فلورسانس و طیف جذبی Uv-Vis مورد استفاده قرار می‌گیرید. می‌توان گفت این روش به منظور اهداف زیر به کار می‌رود:

1. تمایز طیفی: تمایز طیفی یک روش کیفی است که به موجب آن تفاوت‌های کوچک بین طیف‌های تقریبا مشابه آشکار می‌شود.
2. افزایش وضوح طیفی: به کمک طیف‌سنجی مشتق وضوح طیفی افزایش می‌یابد. به این معنی که باند‌های طیفی که همپوشانی دارد را متمایز می‌کند. به این ترتیب می‌توان طول‌موج هر یک از باند‌ها را به دست آورد.
3. آنالیز کمی: این تکنیک، تجزیه و تحلیل چند جزئی را آسان‌تر می‌کند. از طرف دیگر جذب بک گراند (back ground) پس زمینه را تصحیح می‌کند.

طیف مشتق

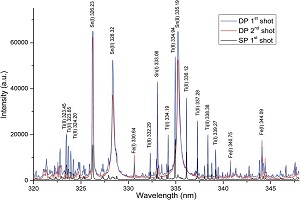
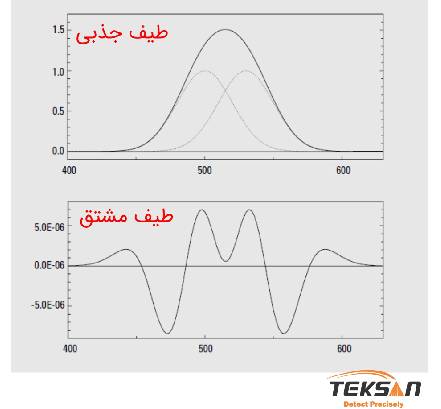
در آنالیزهای کمی، طیف‌های مشتق تفاوت بین باندهای همپوشانی شده را بیشتر نمایان می‌کنند. طیف‌های مشتق مرتبه دوم و یا چهارم، ارتفاع قله‌های موج کوتاه و موج بلند (قله‌هایی که در مجاور پیک اصلی قرار دارند) را اندازه‌گیری می‌کند. شکل ۱ نمونه‌ای از طیف مشتق را نشان می‌دهد.

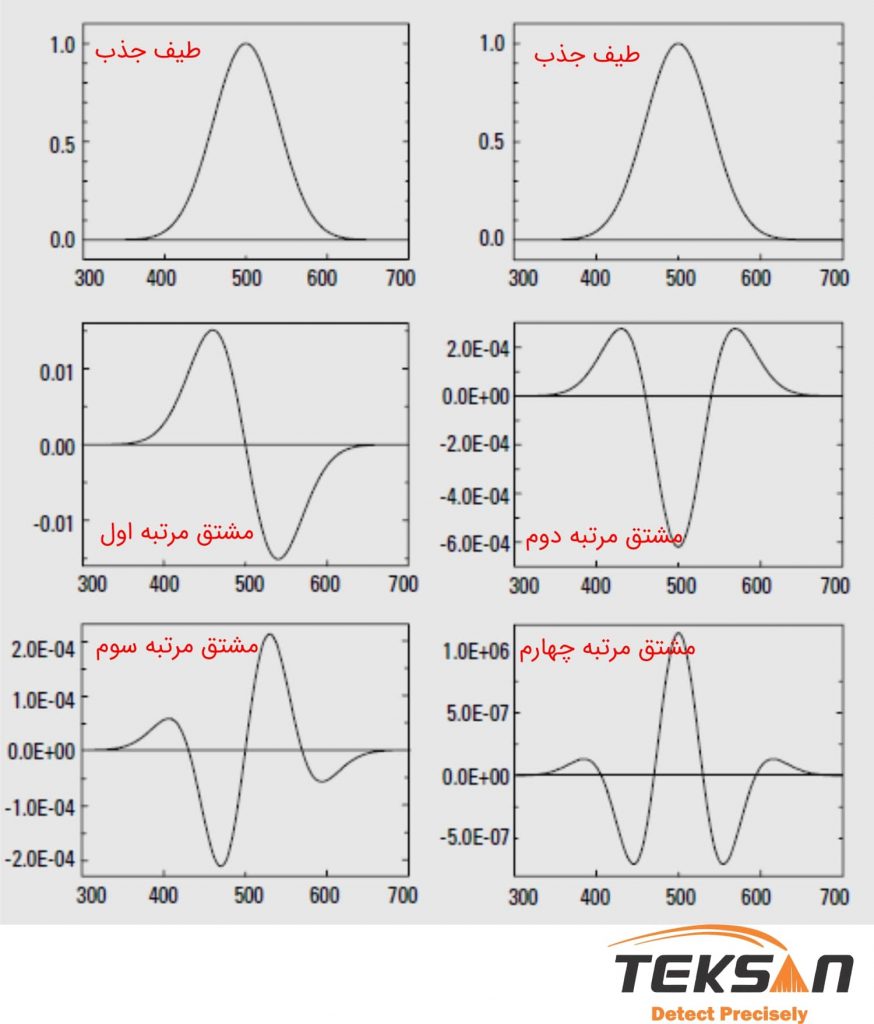
هر مرتبه از طیف مشتق چه چیزی را نشان می‌دهد؟

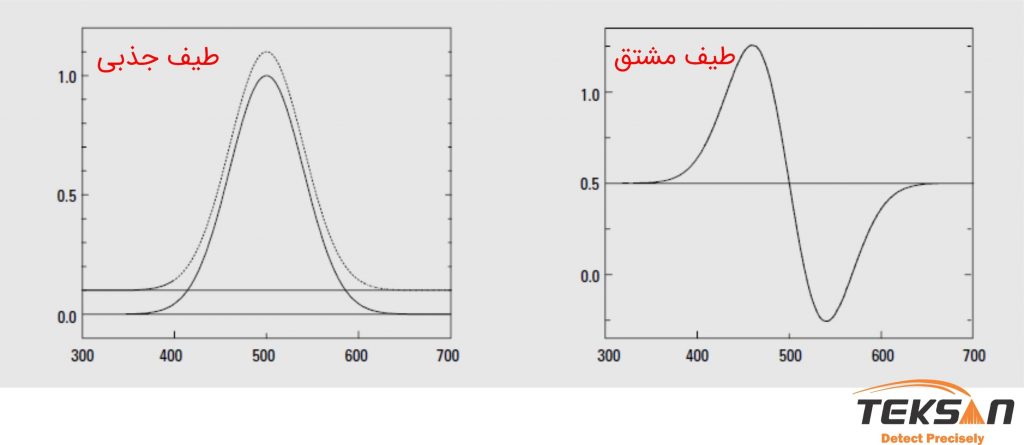
مشتق مرتبه صفر همان طیف اصلی است. همان طور که می‌دانید طیف جذبی میزان جذب نور را به عنوان تابعی از طول‌موج نشان می‌دهد (شکل ۱). مشتق‌های مرتبه اول، دوم، سوم و چهارم مستقیما از طریق مشتق‌گیری از رابطه زیر به دست می‌آیند. هر مقدار که مرتبه مشتق افزایش یابد، میزان حساسیت محاسبات نیز افزایش می‌یابد.

A= f(λ)

مشتق مرتبه اول با یک بار مشتق‌گیری از رابطه بالا به دست می‌آید و در واقع نرخ تغییر جذب بر حسب طول موج را نشان می‌دهد. به شکل ۱ توجه نمایید. در طیف اصلی جایی که λ_max قرار دارد، طیف مشتق مرتبه اول صفر است. طیف جذب مشتق مرتبه اول دارای یک باند ماکزیمم و یک باند مینیموم است.

dA / dλ = f'(λ)

مشتق مرتبه دوم با دوبار مشتق‌گیری از معادله ۱ به دست می‌آید. مشتق مرتبه دوم متناسب با غلظت است. این روش در به دست آوردن طیف مولکولی اتمی و گاز مفید است.

dA^۲/ dλ^۲= f”(λ)

اگر به شکل ۱ دقت کنید خواهید دید که کمینه در همان طول‌موجی است که بیشترین مقدار جذب را در طیف اصلی داشته است. این مقدار کمینه در زیر محور x قرار دارد. علاوه بر این به یاد داشته باشید که تعداد نواحی‌ای که در طیف‌های مشتق دیده می‌شود، برابر با مرتبه مشتق به اضافه یک است.

مشتق مرتبه سوم برخلاف مشتق مرتبه دوم، تابع پراکندگی منحنی اصلی را نشان می‌دهد. مکانی که طیف اصلی دارای قله است، مشتق مرتبه فرد در آن طول‌موج صفر است.

dA^۳/ dλ^۳ = f”'(λ)

مشتق مرتبه چهارم یک طیف معکوس از مرتبه دوم است. به طوری که به جای دره در همان طول‌موج قله مشاهده می‌شود. این قاعده برای مشتق‌های مرتبه زوج صادق است.

dA^۴/ dλ^۴ = f””(λ)

کمی‌سازی

همان طور که می‌دانید طیف اصلی از قانون بیرلامبرت پیروی می‌کند. بنابراین رابطه خطی ساده‌ای بین غلظت و جذب در همه مراتب مشتق وجود دارد:

مرتبه صفر

A=εbc

مرتبه یک

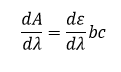
مرتبه n

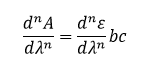
λ طول موج، A جذب، ε ضریب خاموشی، b طول مسیر نور و c غلظت نمونه است.

در طیف مشتق از آن جایی که هم قله در ناحیه مثبت و هم دره در ناحیه منفی وجود دارد، انتخاب طول موج‌ها برای کمی سازی تک مؤلفه‌ای به سادگی خود طیف جذب نیست. مشتقات مرتبه زوج در طول موجی که بیشینه جذب را دارد دارای قله یا دره هستند اما در مشتقات مرتبه فرد، نمودار در این نقطه از صفر عبور می‌کند.

روش به دست آوردن طیف مشتق

طیف‌سنجی مشتق، طیف نرمال را به طیف‌های مشتق مرتبه اول، دوم و غیره تبدیل می‌‌کند. انتخاب مناسب مرتبه مشتق موجب می‌شود تا سیگنال‌هایی که همپوشانی دارند، از هم جدا شوند. مرتبه مشتق، ویژگی‌های یک طیف مانند ارتفاع و عرض سیگنال‌ها و فاصله بین قله‌ها در طیف پایه را مشخص می‌‌کند. طیف مشتق با روش های اپتیکی، الکترونیکی و یا ریاضیاتی قابل استخراج است. روش‌های اپتیکی و الکترونیکی در اسپکتروفتومترهای قدیمی مورد استفاده قرار می‌گرفت اما به تدریج روش‌های ریاضی تا حد زیادی جایگزین آن‌ها شد. از مزایای روش‌های ریاضیاتی می‌توان به سادگی محاسبات با پارامترهای گوناگون و امکان استفاده از تکنیک‌های هموار کردن طیف به منظور افزایش نسبت سیگنال به نویز اشاره نمود.

روش‌های اپتیکی و الکترونیکی

اساس روش اپتیکی بر مبنای مدولاسیون طول موج است. طول موج نور برخوردی به سرعت توسط یک دستگاه الکترومکانیکی در بازه طول موجی با پهنای کم مدوله می‌شود. مشتقات مرتبه اول و دوم با این روش به دست خواهند آمد. از این روش برای اسپکتروفتومترهای با کاربردهای ویژه استفاده می‌شود. مشتق مرتبه اول توسط اسپکتروفتومترهای دوپرتو نیز قابل تولید هستند. طیف مشتق با اسکن هر مونوکروماتور که توسط اختلاف طول موجی کمی جدا شده، ایجاد می‌شود.
در روش الکترونیکی مشتقات مرتبه اول و بالاتر را می توان با استفاده از دستگاه‌های آنالوگ خازن مقاومتی به عنوان تابعی از زمان (هنگامی که طیف با سرعت ثابت در حال اسکن است) تولید کرد.

مشتقات مراتب اول و بالاتر توسط دستگاه‌های آنالوگ خازن مقاومتی به عنوان تابعی از زمان و هنگامی که طیف با سرعت ثابت در حال اسکن است، تولید می‌شوند (dA/dt=S). در این صورت برای مشتق مرتبه اول خواهیم داشت:

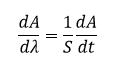
ضعف روش الکترونیکی این است که دامنه و شیفت طول موج مشتقات، با سرعت اسکن، عرض شکاف و ضریب افزایش ظرفیت خازن تغییر می‌کند.

روش‌های ریاضی

برای استفاده از روش‌های ریاضیاتی، طیف با گام‌هایی به اندازه λ∆ دیجیتالی می‌شود. مقدار بازه‌های طول موجی انتخاب شده به دو عامل پهنای طبیعی طیف پردازش شده ((NBW) natural bandwidth) و پهنای طیفی‌ای که توسط دستگاه ایجاد می‌شود، بستگی دارد. عموما برای طیف مرئی-فرابنفش، NBW بین ۱۰ تا ۵۰ نانومتر است. طیف مشتق اول را به سادگی می‌توان با در نظر گرفتن اختلاف جذب، بین دو طول موج نزدیک برای همه طول موج‌ها محاسبه کرد:

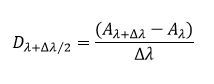
D_λ دامنه مشتق و مقدار متوسط بین دو طول موج جذب است.

برای تعیین مشتق مرتبه دوم، از سه مقدار طول موجی نزدیک به هم استفاده می‌شود:

مشتقات مراتب بالاتر به شکل مشابهی محاسبه می‌شوند. این روش شامل درون یابی خطی ساده بین طول موج های مجاور است.
یک روش بهتر نیز توسط Savitzky و Golay پیشنهاد شده است. برای محاسبه مشتق در طول موج مشخص (λ) تعدادی نقطه (n±) از طیف انتخاب می‌شود و یک چند جمله‌ای با روش حداقل مربعات (the least squares method) برازش (fit) می‌شود:

یکی از مزایای این تکنیک این است که از روش‌های ریاضی برای smooth کردن طیف استفاده می‌شود. در صورتی که مرتبه چند جمله‌ای (l) از تعداد نقاط (۲n+1) کمتر باشد،‌ چند جمله‌ای نمی‌تواند از تمام نقاط داده عبور کند. بنابراین طیف ما هموارتر خواهد شد. این ویژگی می‌تواند موجب افزایش نسبت سیگنال به نویز در فرایند مشتق‌گیری شود. حاصل ضرب ضرایب a_۰…a_l در هر طول‌‌موج و مرتبه فاکتوریل، مقادیر مشتق است: a_۱ مشتق مرتبه اول است، ۲Xa_۲ مشتق مرتبه دوم، ۶Xa_۳ مشتق مرتبه سوم و غیره.

تکنیک Savitzky-Golay روش بسیار کارامدی برای انجام محاسبات است. این روش، اساس الگوریتم مشتق‌گیری در بیشتر دستگاه‌های رایج است. روش‌های دیگری برای محاسبه مشتق (برای مثال انتقال فوریه) نیز وجود دارند اما کمتر مورد استفاده قرار می‌گیرند.
یکی از پیامدهای روش‌های ریاضی برای محاسبات مشتق‌ها این است که نقاط داده در ابتدا و انتهای بازه طول‌موجی در نظر گرفته نمی‌شوند. به عنوان مثال اگر ۵ نقطه به عنوان داده انتخاب شوند یک نقطه از ابتدا و یک نقطه از انتها وارد محاسبات نخواهند شد. بنابراین محاسبات فقط با ۳ نقطه انجام می‌گیرد.
در انتهای این بخش از مطلب می‌توان به نتیجه رسید که اگرچه تبدیل یک طیف Uv-Vis به مشتق مرتبه اول و یا مراتب بالاتر موجب پیچیدگی طیف می‌شود اما محتوای ذاتی آن افزایش نمی‌یابد.
تا این قسمت از مقاله به طور کلی طیف مشتق را بررسی کردیم. در بخش بعدی می‌خواهیم به کاربردهای طیف مشتق بپردازیم. در ادامه خواهیم گفت چگونه و در چه راستایی از طیف مشتق استفاده می‌شود.

کاربردهای طیف مشتق

خطوط نقطه چین در شکل‌های زیر، خط پایه (baseline) را نشان می‌دهند. خطوط خط چین، طیف مؤلفه‌ و خطوط ممتد نشان دهنده طیف آنالیتی است که از طیف مؤلفه تشکیل شده است.

طیف به دست آمده از مشتق

همان طور که در شکل ۱ می‌بینید، هرچه مرتبه مشتق بالاتر می‌رود، تعداد نواحی افزایش می‌یابد و موجب پیچیدگی طیف مشتق می‌شود. افزایش این پیچیدگی در طیف مشتق برای تحلیل‌های کیفی (شناسایی یا مشخصه‌یابی مواد) بسیار سودمند است. طیف‌هایی که در ظاهر بسیار شبیه به هم هستند، تفاوت‌های زیادی در طیف مشتق خود دارند.

وضوح طیفی

همان طور که در شکل ۱ مشاهده می کنید، پهنای باند طیف مشتق مرتبه زوج با افزایش مرتبه کاهش می یابد. پهنای باند طیف مشتق برای شکل گاوسی حدود ۵۳، ۴۱ و ۳۴ درصد نسبت به پهنای باند طیف اصلی در مرتبه‌های دوم، چهارم و ششم کاهش یافته است. این ویژگی در آنالیزهای کیفی برای شناسایی دو آنالیت با مقادیر قله‌های مشابه (که در طیف اصلی دیده نمی شود) بسیار کاربردی است. شکل ۲ این شبیه سازی کامپیوتری را نشان می دهد.

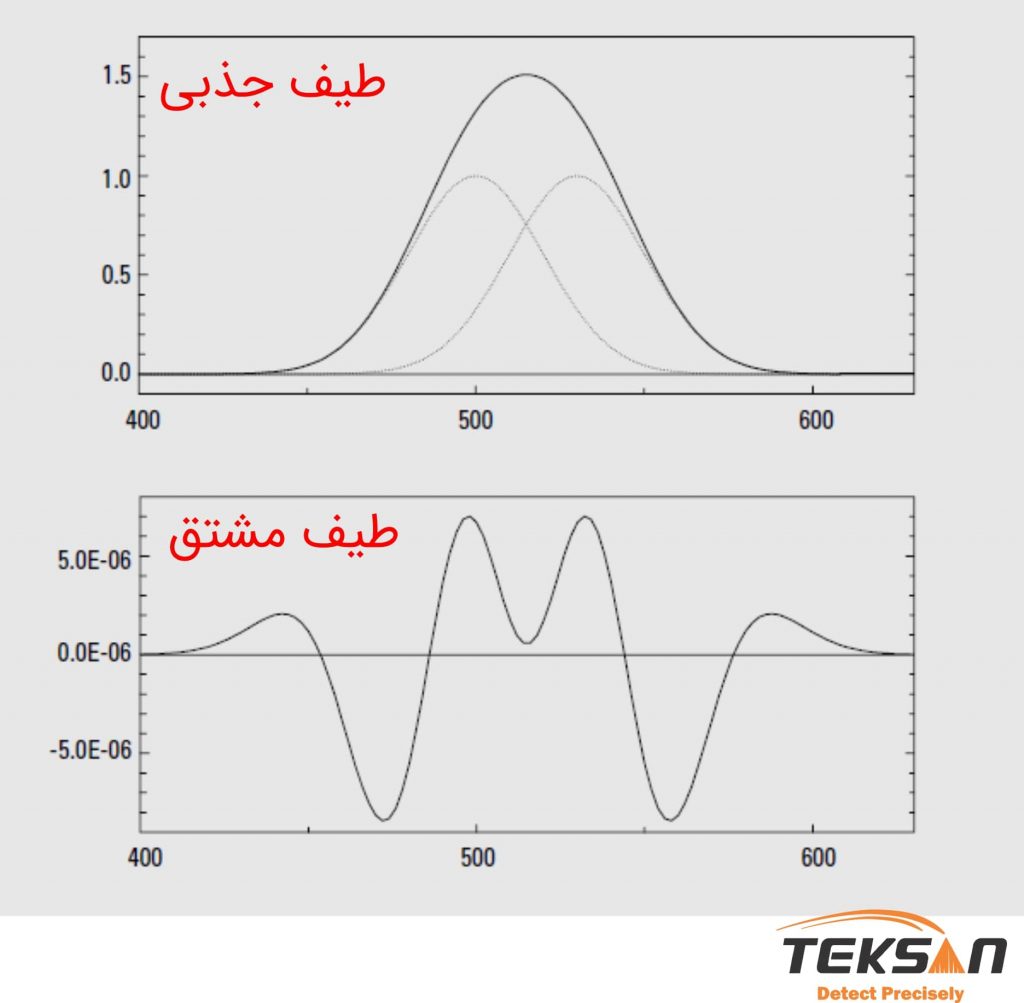
فرض کنید در یک طیف جذب دو قله با پهنای باند طبیعی ۴۰ نانومتر به فاصله ۳۰ نانومتر از هم واقع شده‌اند. این دو قله با توجه به ویژگی‌های دستگاه، یک قله نشان داده می‌شوند. به طوری که عدد جذب نشان داده شده، میانگین عدد جذب این دو قله است. ولی در مشتق مرتبه چهارم، وجود این دو قله به وضوح قابل مشاهده است. البته باید به این موضوع توجه کنید که اگرچه قله‌ها از هم تفکیک شده‌اند اما نمی‌‌توان با اطمینان گفت که این قله‌های تفکیک شده مربوط به دو کروموفور در یک ترکیب منفرد‌اند یا این که مربوط به دو ترکیب هستند. اغلب ادعا می‌شود که افزایش وضوح طیفی و افزایش اختلاف بین طیف‌ها در طیف مشتق، تجزیه و تحلیل چند مؤلفه‌ای ترکیبات با طیف مشابه را امکان پذیر می‌سازد. با این حال همان طور که پیش‌تر نیز اشاره شد، محتوای اطلاعات طیف‌های مشتق از طیف جذبی کمتر است.

حذف پس زمینه

یکی از اثرات رایج در اسپکتروفتومتری، وجود baseline در طیف جذب است. خط پایه یا baseline می‌تواند ناشی از خود دستگاه (عدم پایداری لامپ‌ها یا آشکارساز) یا جابه‌جایی نمونه در اسپکتروفتومترهای تک پرتو باشد. با توجه به این که مشتق مرتبه اول برای جذب با مقدار ثابت صفر است، استفاده از مشتق اول همیشه می‌تواند خط پایه را حذف کند. این موضوع در شکل ۳ نشان داده شده است. سایر اثرات خط پایه که با مشتق مراتب بالاتر متناسب است به شکل زیر محاسبه می شود:

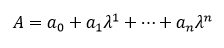
اما باید خاطر نشان کرد که این روش برای حذف baseline مرسوم نیست.

تمییز دادن

با توجه به اینکه در فرایند مشتق‌گیری طیف‌های پهن توسط قله‌های نوک تیز فرو نشانده می‌شوند، این موضوع با افزایش مرتبه مشتق افزایش می‌یابد. منشأ این اثر را توضیح می‌دهیم:

دامنه Dⁿ برای یک طیف گاوسی در n^th مشتق با پهنای باند W نسبت عکس دارد:

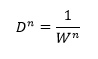
برای دو طیفی که پهنای طیفی متفاوت اما با شدت برابر در مرتبه صفر دارند، دامنه مشتق طیف با پهنای کمتر (X)، بیشتر از طیف با پهنای بزرگتر(Y) است. (مشتق مرتبه nام)

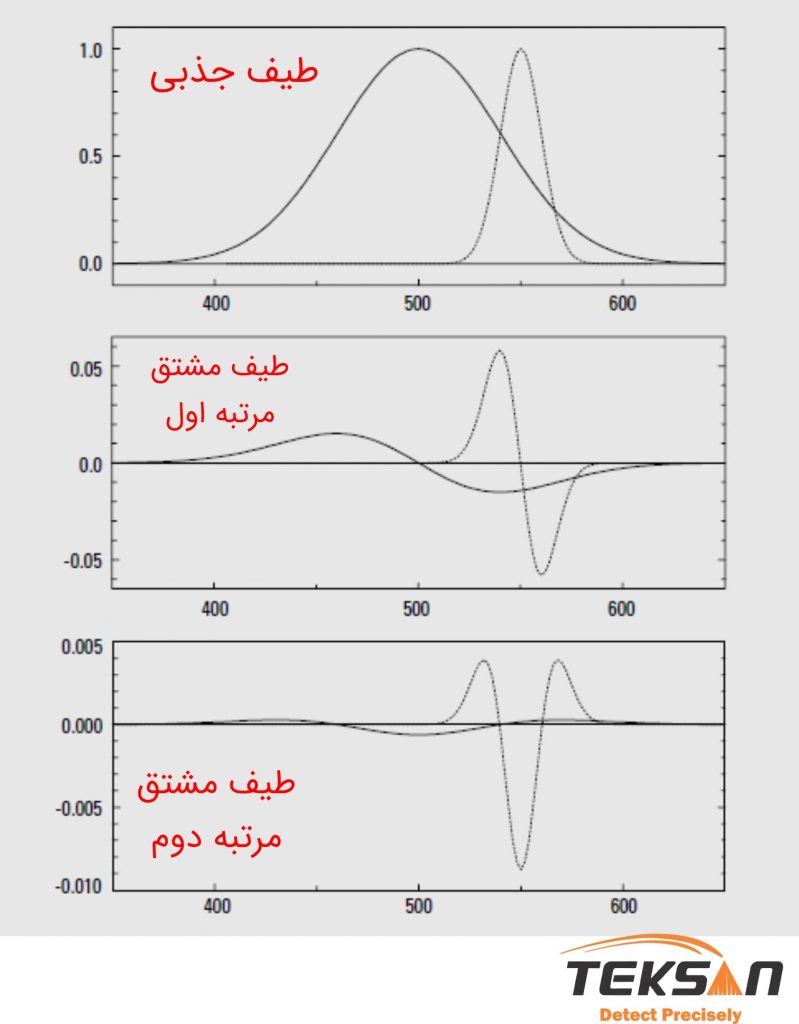
شکل ۴ این اثر را به خوبی نشان می‌دهد. دو قله یکی با پهنای باند طبیعی ۱۶۰ نانومتر و دیگری با پهنای باند طبیعی ۴۰ نانومتر داریم. این دو قله در طیف اصلی دامنه یکسانی دارند. در مشتق اول قله باریک‌تر دامنه ۴ برابری و در مشتق دوم دامنه ۱۶ برابری دارد. از این ویژگی برای افزایش دقت کمی سازی در مواقعی که یک قله باریک در حضور یک قله پهن وجود دارد استفاده می‌شود تا اثرات خطای ناشی از پراکندگی را کاهش دهد.

پراکندگی یک مسئله رایج در طیف‌ سنجی است که ذرات معلق درون نمونه آن را ایجاد می‌کنند. پراکندگی متناسب با نوعی که دارد با معکوس توان چهارم (رایلی، ذرات کوچک) و یا دوم (تیندال، ذرات بزرگ) طول موج متناسب است. از آن جایی که این رابطه معکوس است، مشتق گیری نمی‌تواند اثر پراکندگی را از طیف حذف کند. اما استفاده از طیف مشتق می‌تواند اثر آن را در محاسبات کمی کاهش دهد.
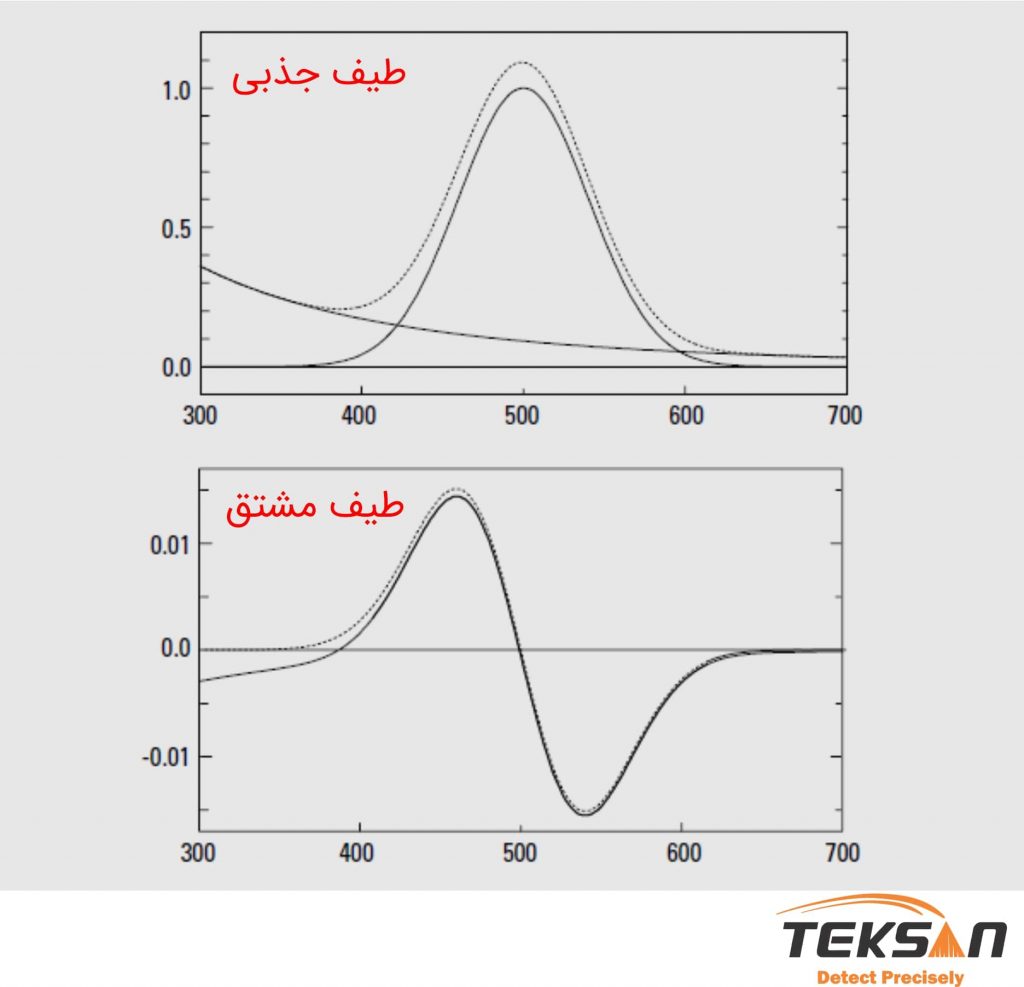
شکل ۵ یک قله با پهنای باند طبیعی ۴۰ نانومتر و قله‌ای مشابه را در حضور یک پس زمینه ناشی از پراکندگی نشان می‌دهد. بدون هیچ تصحیحی، به دلیل وجود اثر پراکندگی، عدد دامنه در ۵۰۰ نانومتر ۱.۰۹۲۰ است. در صورتی که این مقدار باید ۱.۰۰ باشد. محاسبات در این طول موج خطای ۹.۲ درصدی را نشان می‌دهد. با استفاده از مشتق اول، اثر پراکندگی کاهش می‌یابد. سیگنال در حضور پراکندگی ۰.۲۹۹۲ است که با ۰.۰۳۰۲۴ تفاوت کمی دارد و فقط خطای ۱.۱ درصدی را نشان می‌دهد.

ترکیب عوامل مخدوش کننده طیف

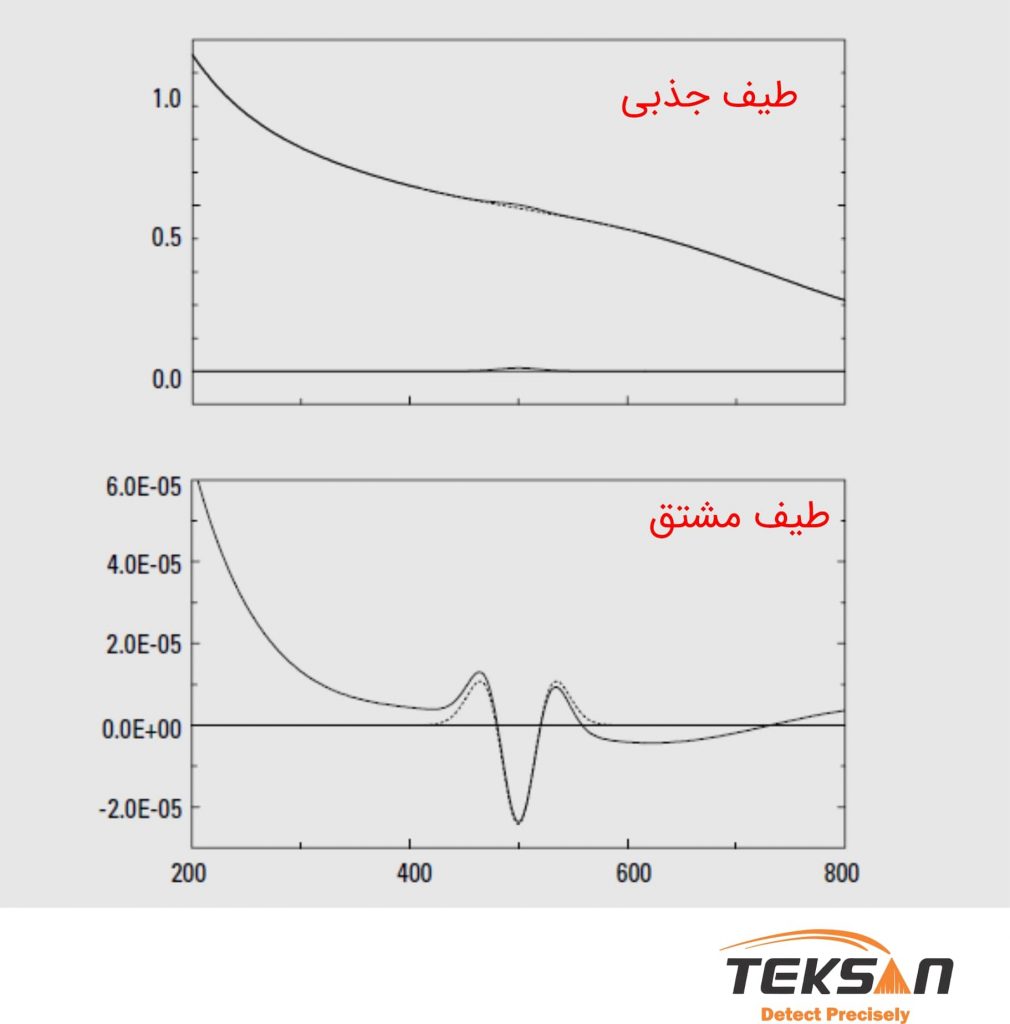
توجه کنید که وجود خط پایه همیشه به دلیل پراکندگی و یا عوامل دیگری مانند جذب‌های ناخواسته نیست. گاهی ترکیب این عوامل با هم موجب ایجاد یک پس زمینه می‌شود که در طیف جذب به خوبی قابل شناسایی نیست. اما در طیف مشتق به خوبی قابل مشاهده است. در شکل ۶ این اثر به خوبی دیده می‌شود.

ملاحظات مربوط به دستگاه

امروزه عملا تمامی دستگاه‌های اسپکتروفتومتر قادرند تا طیف مشتق را با محاسبات ریاضی به دست بیاورند. بنابراین در این مطلب در رابطه با ملاحظات دستگاه برای روش‌های اپتیکی و الکترونیکی صحبت نمی‌کنیم. به طور کلی الزامات دستگاه برای طیف‌سنجی مشتق مشابه دستگاه معمولی طیف‌سنجی است؛ اما امکان تکرارپذیری (reproducibility) طول موج و نسبت سیگنال به نویز از اهمیت بیشتری برخوردار است.
زیاد شدن رزولوشن طیف‌های مشتق شده نیازمند این است که تکرارپذیری طول موج اسپکتروفتومتر شما بالا باشد. در حالت مشتق خطاهای طول موجی کوچک، می‌تواند منجر به خطاهای سیگنال بزرگتری نسبت به حالت جذب شود. اگر اسپکتروفتومتر بتواند پیش از مشتق‌گیری طیف را اسکن و میانگین گیری نماید، نسبت سیگنال به نویز افزایش می‌یابد.
در فرایند مشتق‌گیری توانایی کنترل میزان Smoothing نمودار برای تحلیل‌های مختلف اهمیت دارد. در تئوری Savitzky-Golay این به معنی انتخاب بهینه درجه چند جمله‌ای و تعداد نقاط است.

نسبت سیگنال به نویز

یکی از اثرات ناخواسته در فرایند مشتق‌گیری این است که نسبت سیگنال به نویز با افزایش درجه مشتق، کاهش می یابد. زیرا نویز همیشه به صورت قله‌های تیز در طیف دیده می‌شود. بنابراین اگر اطلاعات طیفی استفاده شده در محاسبات مشتق فاصله‌های ۲ نانومتری داشته باشند، نویز به اندازه ۲ نانومتر پهنای باند خواهد داشت. اگر طیف آنالیت ۲۰ نانومتر پهنا داشته باشد، نسبت سیگنال به نویزِ مشتق اول ده برابر کمتر از طیف اصلی خواهد بود. اثر کاهش نسبت سیگنال به نویز می‌تواند با هموار کردن طیف با استفاده از برازش چند جمله‌ای کاهش یابد. اما باید توجه کرد که هموار کردن زیاد می‌تواند موجب تحریف طیف مشتق شود. اگر اسپکتروفتومتر بتواند میانگین‌گیری را انجام دهد قبل از مشتق‌گیری می‌توان این نسبت سیگنال به نویز را بهبود بخشید.
با توجه به این که با کاربردهای طیف‌سنجی مشتق آشنا شدید، اکنون وقت آن رسیده که مزایا و معایب این روش را بررسی کنیم.

مزایای طیف‌ سنجی مشتق

به طور کلی می‌توان مزایای طیف‌گیری مشتق را به صورت زیر بیان کرد:

• حضور دو قله که همپوشانی دارند، حتی در محدوده کوچکی از طول موجی قابل تشخیص است.
• حضور قله‌های کوچک و ضعیف در کنار قله‌های قوی قابل شناسایی است.
• اثرات پس زمینه طیفی را کم می‌کند.
• حتی در صورت وجود پس زمینه، تجزیه و تحلیل کمی را می‌توان مورد مطالعه قرار داد. زیرا رابطه بین مقادیر مشتق و سطوح غلظت خطی است.

معایب طیف سنجی مشتق

یکی از معایب این تکنیک این است که به پارامترهای مختلف بسیار حساس است. این روش تنها محدود به سیستم خاصی است و به دلیل تکرارپذیری کمتر، کاربرد محدودی دارد. در اندازه‌گیری طیف‌های متقاطع صفر دقت کمتری دارد. باتوجه به شباهت‌هایی که طیف‌های مشتق و طیف مرتبه صفر دارند، تغییرات کوچک در یک طیف پایه می‌تواند به شدت طیف مشتق را تغییر دهد. تکرارپذیری این روش بسیار کم است.

جمع‌ بندی

ما در این مقاله سعی کردیم تا کلیات طیف‌سنجی مشتق را پوشش دهیم. به همین منظور ابتدا مفهوم طیف‌سنجی مشتق را شرح دادیم. سپس روش‌های به دست آوردن این طیف را بررسی کردیم. در مرحله بعد برای اینکه با این مفهوم بیشتر آشنا شوید کاربردهای طیف‌سنجی مشتق را مورد مطالعه قرار دادیم. در آخر نیز مزیت‌ها و معایب این طیف‌سنجی را بررسی کردیم.

منابع

۱- https://zaya.io/zy0x3

۲– https://zaya.io/xc2si